Author Archives: Peter

We’re hiring!

Two permanent positions in pure maths. One in geometry/topology, one open for all areas of pure mathematics. Applications are through mathjobs (link to Job 1, link to Job 2), and are due December 18 (AEDT).

I’ve never been at ease with the Jacobson density theorem, every proof that I’d seen felt somewhat weird and never had any stickiness in my mind. So I came up with my own proof, I hope you like it.

The Theorem (Jacobson Density Theorem}
Let be a field and a -algebra (yes unital). Let be a finite dimensional simple -module and (which is a division algebra by Schur’s Lemma). Then the canonical homomorphism from to is surjective.

Proof
First, without loss of generality (replacing by a quotient), we can assume that is faithful.

Let us first deal with the case when is a division algebra. Then . And as well, acting by right multiplication. And we are done.

Since is not a division algebra it has a non-zero element which is not invertible.

If is not nilpotent, then the minimal polynomial of factors as where . In particular it has two coprime factors, so by the Chinese remainder theorem has a non-trivial idempotent. In particular, contains a non-trivial idempotent.

If on the other hand is nilpotent, then we can find with , and . Since is irreducible, there exists with . Then and . So is not nilpotent, and we can run the argument of the previous paragraph again to conclude that contains a non-trivial idempotent.

Let be this non-trivial idempotent. We will use the fact that is an irreducible -module. This is part of a general fact, that is a bijection betwen simple -modules with and simple -modules. Furthermore, from the nature of the constructions of both directions of this bijection, we can conclude that

Now we can perform an induction on dimension. The inductive hypothesis tells us that and are both surjective. To finish, given the symmetry between and , it suffices to show that given any -hyperplane with and any -line , there is a nonzero element in with kernel and image . (I thought about this step myself in terms of matrices, but actually writing it up like that feels a little gauche).

The inductive hypothesis applied to allows us to find a nonzero element with . Pick nonzero and . Since is simple there exists with . Then does the trick and our proof is complete.

The following quote is by Matt Emerton (in a comment on MathOverflow)

I think there is a genuine tension between proofs that a professional will like (where professional here may mean professional algebraist!) and ones that are elementary. For professionals, reductions and devissages are easy, natural, and we don’t even think of them as real landmarks in the proof; they are just serve as passages between the key points and ideas. But in writing things out, they can take a lot of words, and seem (as you wrote) mysterious and difficult. I don’t know the best way to deal with this tension.

Interestingly, Matt posted it as part of a discussion about exactly what I wanted to talk about in this post, the teaching of the structure theorem for finitely generated abelian groups, or more generally, of finitely generated modules over a PID.

My personal connection is that I taught this as part of our third-year algebra course this year at the University of Melbourne, and am slated to do so again next year. I think that I did not do a particularly good job of teaching it in 2022, primarily because I got distracted by the reductions and devissages and tried to proceed along those lines as much as possible, when what I have learned is more appropriate for one of these courses is the more prosaic approach involving matrix manipulations. It is with the matrix manipulations (directly proving Smith Normal Form) that I plan to teach this part of the course in 2023 (and beyond, if necessary).

For completeness, allow me to state the professionals’ proof: Split off the quotient by the torsion subgroup to reduce to the torsion case. Then canonically decompose the module into a direct sum of its p-primary components. Then use the fact that is injective over itself to manually split the remaining short exact sequences needed to complete the classification.

While it may not be reasonable to expect a third-year student to follow this proof, I think it is fair to expect any PhD student of mine to be able to understand and execute this proof.

The Simon Marais Mathematics Competition happened last weekend. It is a maths competition for undergraduate students across Europe, Asia, Africa and Oceania. This post is about problem A4, which I submitted. I’ll talk a bit about where the problem came from, a generalisation, a conjecture and also provide a solution. The entire paper is available on the Marais website, and solutions should be put up there at some time in the near future.

Problem (SMMC 2022 A4)
Let be a positive integer, and let 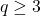be an odd integer such that every prime factor of 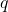is larger than . Prove that

is an integer that has no prime factor in common with .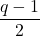

Origins

Let 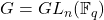and let 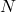be the subgroup of monomial matrices (a matrix is a monomial matrix if and only if it has exactly one nonzero entry in each row and column). I show below in my solution that this question is equivalent to the fact that the integer 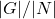is coprime to 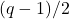. Now why would I ever care about that?

This coprimality fact implies that the cohomology of 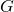with mod 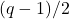coefficients is isomorphic to the cohomology of 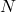with mod 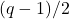coefficients. And I was interested in these cohomology groups because the second cohomology group classifies central extensions, which is what I used to think about back in my PhD days. The group 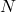feels somewhat more “combinatorial” than 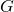, so it is nice to be able to pass information from 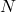to 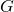for free.

Generalisations (known and conjectural)

Let 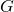be a split reductive group over 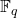, which I conflate with its 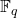-points below in an abuse of notation. Let 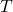be a maximal split torus and 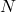its normaliser in 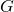. Then

Here 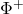is the set of positive roots and the collection of integers 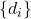are the exponents of the Weyl group. Then the same argument as in my proof below shows that this fraction is an integer, relatively prime to .

If we remove the assumption that 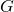is split, then I suspect the same conclusion is satisfied, but there is an additional argument needed as the formula for the quotient has additional factors. I have not worked out this argument and really don’t want to resort to case by case arguments, so there is your conjecture (I expect we now need to say 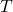is a maximal torus containing a maximal split torus).

Solution

First we show that the fraction in the question is an integer. Since divides 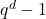as a polynomial for all , the statement only depends on the residue class of 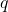modulo 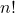. Since every prime factor of 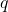is greater than , 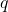is relatively prime to 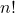. So by Dirichlet’s theorem on primes in arithmetic progressions, we may assume without loss of generality that 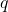is prime.

Let 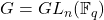and let 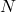be the subgroup of monomial matrices. Then

By Lagrange’s theorem 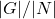is an integer. Since 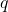is relatively prime to 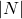, we can further divide by the largest power of 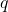in 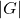and deduce that

is an integer.

Now let 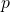be a prime dividing and let be a positive integer. To conclude, it suffices to show that the fraction

has zero 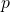-adic valuation. Write 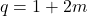, then by the binomial theorem,

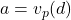Let and 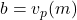. Since 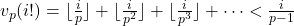, we get

We have the inequality 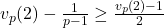, so

For 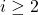, we therefore get

as 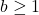from our assumption that 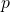divides .
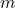Thus in our sum, the term with 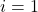has a strictly smaller 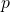-adic valuation than every other term, so determines the 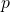-adic valuation of the sum, and we get

completing the proof.

This is a quick note to prove that two bases of an infinite dimensional vector space have the same cardinality. We freely use the axiom of choice and other standard facts about cardinalities of infinite sets. We will in fact prove the following:

Theorem: Let be a vector space with basis with an infinite set. Let be a linearly independent subset of . (e.g. a basis of a subspace). Then .

To prove this, WLOG is a basis of (by extending to a basis of if necessary). For all , write

Let be the set of pairs with . Then has finite fibres, since the sum above is finite, and is surjective, since the lie in the span of the with in the image of , but also the generate . Since is assumed infinite, this is enough to prove that , as required.